범주형 자료 분석 본문
************************************************************************************************************
INDEX
** 적합도 검정
** 독립성 검정
** 동일성 검정
************************************************************************************************************
범주형 자료에 대한 통계적 추론 방법
> 언제 어디에서 쓰는지 숙지하여라
> 교차 분석, 카이제곱 분석 등으로 불리기도 한다
* 범주형 자료 ( categorical data )
> 명목 변수라고도 하며
> 관측된 결과를 어떤 속성에 따라 몇 개의 범주로 분류시켜 도수로 주어진 데이터
* 범주형 자료 분석 ( categorical data analysis )
> 범주형 자료에 대한 통계적 추론 방법
> 카이제곱 검정으로 추론함
ex) 남여 성별에 따라서 선호하는 핸드폰 회사가(의 비율)이 동일한가?
** t-test와 카이제곱 검정의 차이
> t-test 는 연속형 변수의 차이에 대한 검정
> 카이제곱 검정은 명목형 변수에 대해서 사용
*******개념*************************************************************************************************
*** 세 검정 모두 귀무가설은 "~하다", 대립가설은 "~하지 않다."임.
** 적합도 검정 ( goodness of fit test )

> 관측된 값들이 추론하는 분포를 따르고 있는지 검정, 한 개의 요인만을 대상으로 검정
> 추론하는 분포와 해당하는 속성 -> 귀무가설에서의 잡종 비율 1:1:2와 속성:조사한 잡종 비율 25:20:55 간의 적합도 검정
ex) 멘델의 유전 법칙에 부합하는지 검사하기 위해 테스트할 때, 완두콩의 잡종 비율이 ㄱ:ㄴ:ㄷ = 1 : 1 : 2 였다고 가정해 보자.
100개의 콩을 조사한 결과 까 25 ㄴ가 20 ㄷ가 55개였다면 앞선 가정이 맞는지 유의수준 0.05에서 검정해보자
** 독립성 검정 ( test of indepence )

> 관측된 값을 두개의 요인으로 분할하고 각 요인이 다른 요인에 영향을 끼치는지(독립)를 검정
> 속성 A와 B는 영향이 있는지 없는지
> 기본적으로 2 * 2 보다는 큰 범주에서 사용한다
> degree of freedom = (row-1)(column-1)
> 지지하는 정당과 사는 지역 ( a,b,c 구)는 관련이 있는지 알아보기 위해서 1000명을 뽑아서 조사한 자료가 있을 때,
지지 정당과 사는 지역이 독립인지 유의수준 0.05 수준에서 검정해보자
** 동질성 검정 ( test of homogeneity ) -- 독립성 검정과 방식은 동일, 설계만 다름
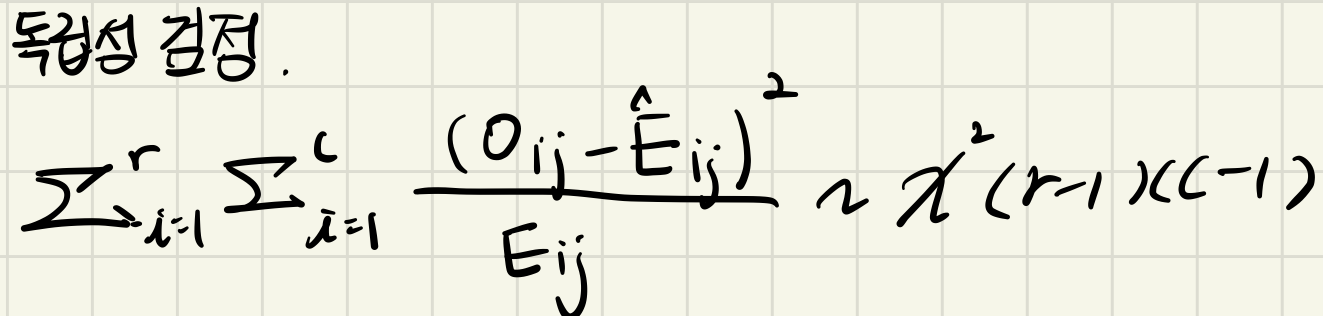
> 분할표 상의 두 변수에 대해서 3개 이상의 속성의 모집단 비율이 같은지
> 동질성 검정과는 가설에서 차이가 나고, 검정 방법은 같다.
> 독립성 검정과는 달리, 비교할 두 변수 각각의 표본의 크기를 같게 해야한다 -> 남자 100명 여자 100 명 계 200명.
> degree of freedom = (row-1)(column-1)
> 남녀의 핸드폰 선호가 제조사별로 동일한지 조사하기 위해서 남자 100명 여자 200명을 조사하였다. 유의 수준 0.05에서 동일한지 검정해보아라.
********예제************************************************************************************************
** 적합도 검정 +
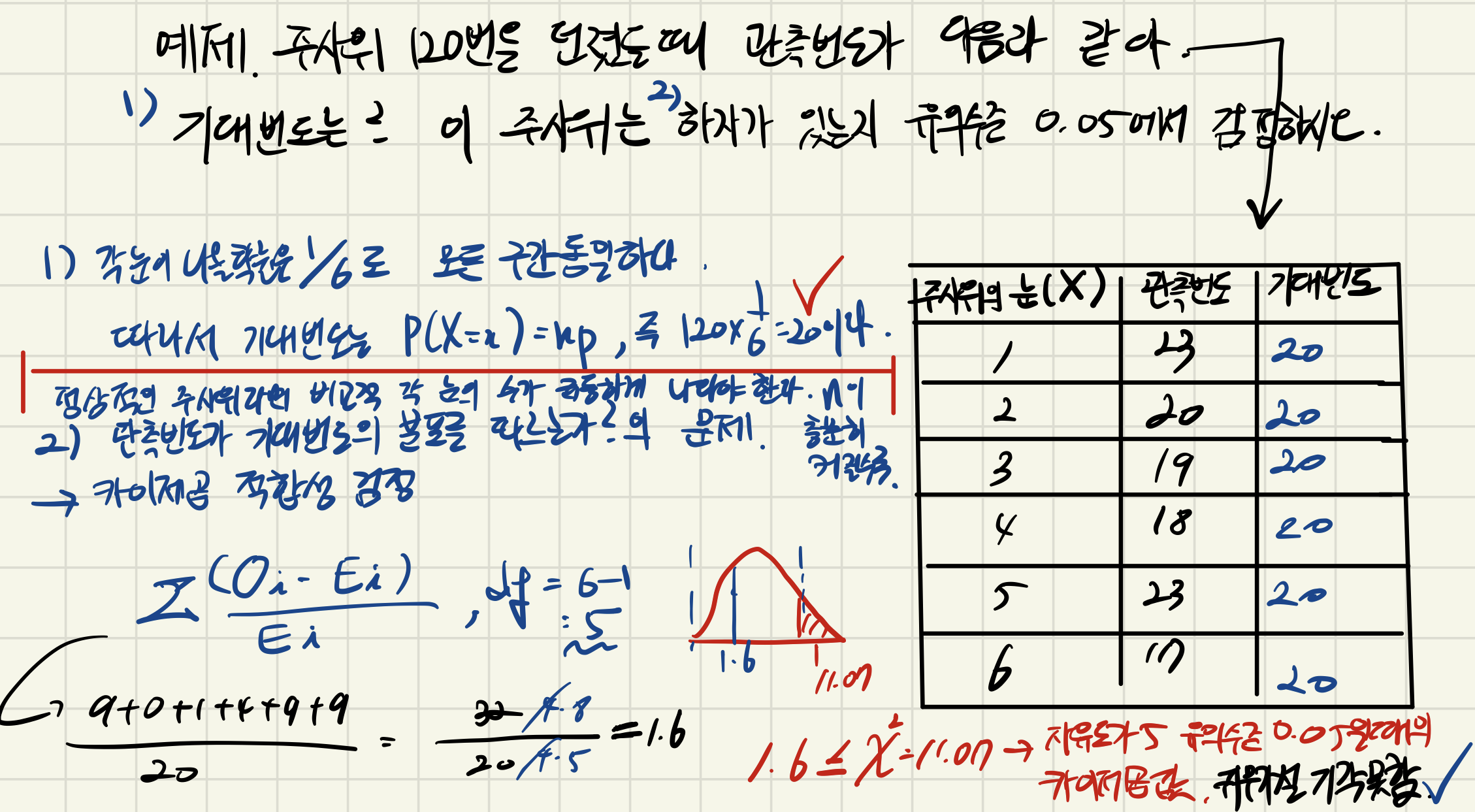
> 수기로 푼 것과 동일하게 나오는지 확인해보자
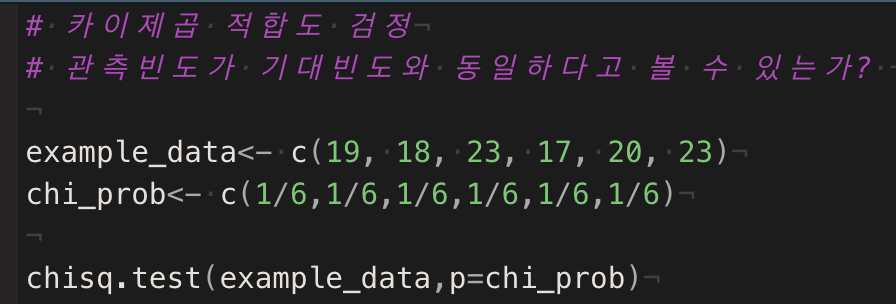
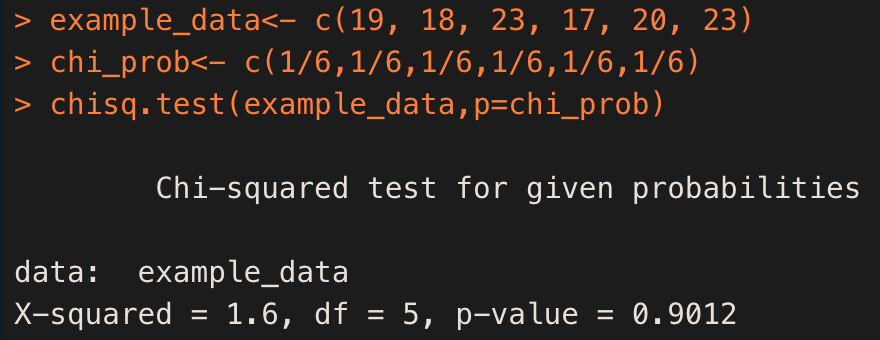
chisq 값은 ( 분포표 ) 1.6이고 n=6에서 자유도는 5이며 parameter -1(적합도 검정은 한개의 요인)
p-val 은 0.9012>=0.05 로 귀무가설을 기각할 수 없다.
** 독립성 검정 +
예제 ) 각 셀의 기대빈도 Ei 구하기
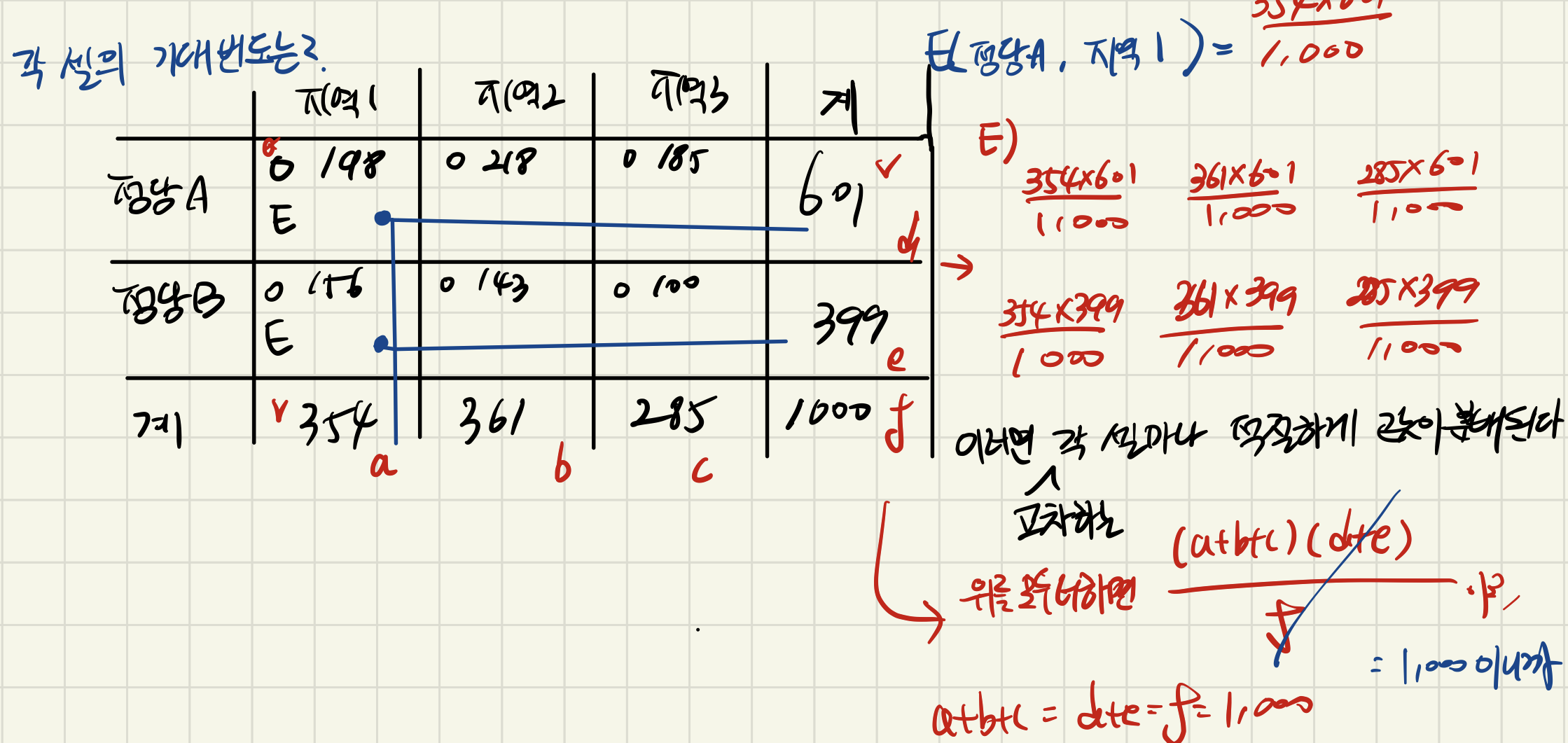
** 동질성 검정 +
> 서로 다른 모집단에서 관측된 값들이 범주 내에서 동일한 비율을 나타내는지 검정
> 가설 H0 : 남녀간에 선호하는 핸드폰 제조사는 동일하다 vs H1 : 남녀간에 선호하는 핸드폰 제조사는 동일하지 않다
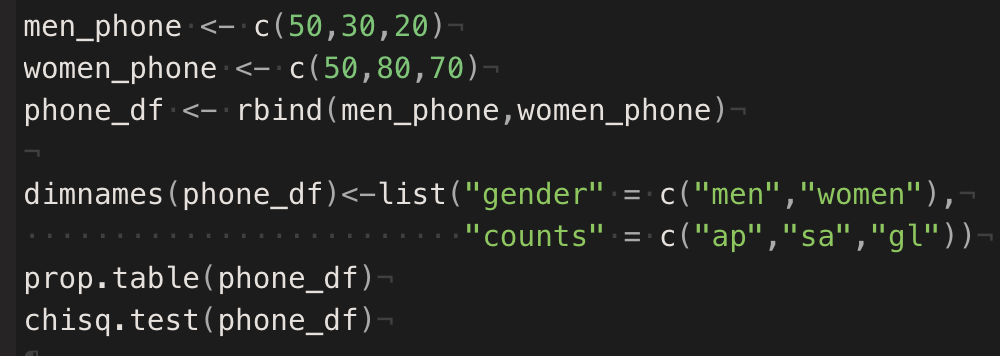
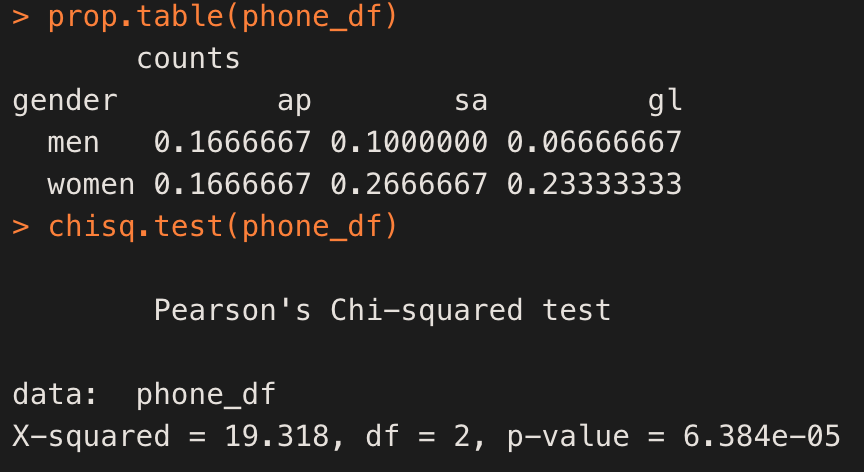
> prop.table 로 내부 비율을 확인 -> 이후 검정!
> degree of freedom = (row-1)(column-1) = (2-1)(3-1) = 2
> p-val < 0.05로 귀무가설을 기각! 남녀간에 선호하는 제조사는 같다고 볼 수 없다.
* 일반적으로 회사에서 분석하고 있는 방식은?
sql(데이터 다운로드) + 엑셀(피벗 테이블)
* 어떤 관점에서 분석을 해야 하는가?
* 통계청 DB
국가통계통합DB 호스팅 통계DB시스템
stat.kosis.kr
* 시간의 흐름에 따라서 어떤 산업이 거래액이 증가하고 있는가?
-> ex) colum을 time ( t ) , 산업군을 row
-> 비중변화를 알 수 있음
-> 여러 산업군의 월별 비율을 비교해보면, 해당 산업에서는 비율이 늘었어도, 전체 산업을 놓고 비율을 비교해봤을때 줄었을 수도 있다
-> 이런 관점을 가지고 검정을 해볼수가 있다.
'BF 2024 > 통계' 카테고리의 다른 글
| 단순 회귀분석 (0) | 2022.02.15 |
|---|---|
| 기본적인 통계분석의 갈래 , when what how (0) | 2022.02.15 |
| 상관관계 (0) | 2022.02.15 |
| 가설검정 (0) | 2022.02.15 |
| 추정 ( 개념, 점 추정과 구간 추정과 신뢰구간, 허용 오차와 표본 크기 ) (0) | 2022.02.15 |



