상관관계 본문
** 상관관계 ( correlation coefficient )
> 두 변수간의 함수 관계가 선형적인 관계가 있는지 파악할 수 있는 측도, 상관계수

1) 상관계수 -1 =< p <= 1
2) 상관계수가 1에 가까울 수록 강한 양의 상관관계이다
3) 상관계수가 -1에 가까울 수록 강한 음의 상관관계이다
4) 상관계수가 0에 가까울수록 두 변수 간의 상관관계가 약하다는 것
5) 상관계수가 0이라는 것은 두 변수간의 상관관계가 나타나지 않는다는 것이다
** 해석에 있어서 주의할 점!
> 상관계수는 두 변수간 상관관계에 대한 수치일 뿐이다. 실제 그 둘의 상관관계도 그렇다고 확신할 수는 없다.
** 공분산의 경우 (데이터를 - 기대값) / n-1으로 나누어 주어, 단위에 따라 편차가 심했을 수 있지만
상관관계의 경우 공분산을 다시 두 변수의 표준편차로 나누어 주어 편차를 normalization 하는 효과가 있다
** 표본 상관관계 ( sample correlation coefficient ) , 변수 타입에 맞게 상관계수를 산출해야 한다
* 모수적 상관관계 ( 피어슨 ) .. 모피어스
* 비모수적 상관관계 ( 스피어만 , 켄달의 타우) ...비모스피어만로 외웠었다
** 모수적 상관관계 - 연속형과 연속형 척도의 변수로 정규분포로 구할 수 있는 선형관계이다. -> 변수가 정규분포(정규성)충족해야한다!!
* 피어슨 상관계수 ( 등간척도나 비율척도의 자료형, 공분산을 각각의 표준편차로 나눈다 ) 와 검정통계량
* 상관계수 구하기
> 평균과 표준편차를 구하고 R_xy 시그마로 r값을 구한다.
> 이후 검정통계량 수식의 R과 N(자유도, 샘플 수 - 변수param의 수 )에 대입하여 t분포로 값을 구한다


* 가설 수립 : H0 : p = 0 vs H1: p != 0
> 귀무가설: 두 변수간의 상관관계가 없다 , 연구가설 : 두 변수간의 상관관계가 존재한다
* 다양한 상황에서의 상관계수에 따른 산점도

> "상관계수는 두 변수간 선형적 관계를 수치로 표현한 것으로서 " 선형관계에 가까울 수록 1이다. 산포되어있으면 수치가 낮다
> 맨 밑의 다양한 도표처럼 상관계수는 0(상관관계가 없다)이고 변수간 독립관계가 아닌 경우도 있다
* 비모수적 상관관계 ( 스피어만 , 켄달의 타우)
* 스피어만 상관계수
> 단순 증감에 대한 상관관계 정도를 파악할 수 있다.
> 비정규적인 관계인 만큼, 순위정보에 대한 통계적 의존성에 대해서만 정보를 준다. 순서정보(서열척도)를 분석하는데 사용.
> 다만 선형적 관계를 파악하지는 못한다.
> 연속형 자료에 이상치가 두드러질 경우 순위정보만을 이용할 때 사용할 수 있다, 또 자료가 너무 적을때도 활용 가능하다.
* 두 변수 Xi Yi를 정렬하여 순위대로 Ri , Si 라고 하고 , 순위 정보와 순위 평균, 표준편차 등 순위 자료 만을 피어슨 상관계수에 대입.
* 순위 정보는 연속형 데이터보다 자료를 덜 포함하고 있기 때문에, 선형 관계가 약해도 둘다 증가하거나 감소하면 |rs는 = 1|에 가까워질 수 있다.
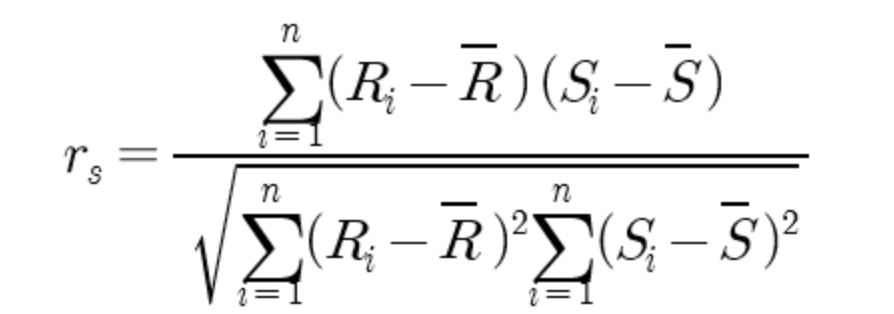
* 켄달의 타우
> 역시 비모수적 상관계수 산출 기법
> 특정 자료의 두 변수간 순서쌍을 기준으로 순위 상관계수를 매기는 기법
> ( concordant pair - disconcordant pair ) / 1/2 { n*(n-1) }
> concordant pair + disconcordant pair = 1/2{ n*(n-1) } 개 ,
> 즉 cp - dcp / cp + dcp 로 표현할 수 있다
> xi < xj, yi < yj 또는 xi > xj, yi > yj가 성립하면 부합, xi < xj, yi > yj 또는 xi > xj, yi < yj면 비부합이라고 정의한다. 즉, x가 커질 때 y도 커지면 부합concordant, x가 커질 때 y가 작아지면 비부합discordant이라고 본다.
ex)
no1. no2. no3. no4. no5
height. 1. 3. 2. 5. 4
weight. 1. 2. 4. 3. 5
모든 순서쌍, 그러니 무방향성 노드가 5개 있다고 생각하자. 1/2( n* n-1) 개의 순서쌍이 있다.
(n1 and n2 ) , (n1 and n3 ), ( n1 and n4 ), (n1 and n5 ) , ( n2 and n3 ), (n2 and n4 ) .......(n4 and n5 ) 를 각각 모두 비교한다.
> 구조상 데이터가 많이 부합할 수록 1에 가까운 수치가 나올 것이다.
> 반면 비부합 순서쌍이 전부일 경우 -1에 가까운 수치가 나올 것이다.
'BF 2024 > 통계' 카테고리의 다른 글
| 기본적인 통계분석의 갈래 , when what how (0) | 2022.02.15 |
|---|---|
| 범주형 자료 분석 (0) | 2022.02.15 |
| 가설검정 (0) | 2022.02.15 |
| 추정 ( 개념, 점 추정과 구간 추정과 신뢰구간, 허용 오차와 표본 크기 ) (0) | 2022.02.15 |
| 모집단과 표본 분포 (0) | 2022.02.15 |



