이산형 확률 분포 ( 균등, 베르누이, 이항, 포아송, 기하, 음이항 분포 ) 본문
************************************************************************************************************
INDEX
이산형 확률 분포
** 이산형 확률분포에서의 균등 분포 ( discrete uniform distribution )
** 베르누이 시행 , Bernoulli trial : 각 시행의 결과가 성공, 실패 단 두가지 결과만 존재하는 시행.
** 베르누이 분포 ( Bernoulli distribution )
** 이항분포 ( Binomial distribution )
** 포아송 분포 ( Poisson distribution )
** 이항 분포의 포아송 근사
** 포아송 분포의 조건
** 기하 분포
** 음이항 분포
************************************************************************************************************
<< 이산형 확률 분포 >>
* 이산형 균등 분포 ( discrete uniform distribution ) : 확률 변수 x개 유한개이고, 모든 확률 변수에 대하여 균일한 확률을 갖는 분포.

* 베르누이 분포 ( Bernoulli distribution )
> 베르누의 시행에서 확률 변수 X의 분포를 베르누이 분포라고 한다.
> 베르누이 시행 , Bernoulli trial : 각 시행의 결과가 성공, 실패 단 두가지 결과만 존재하는 시행.

* 이항분포 ( Binomial distribution )
* 연속적인 베르누이 시행을 거쳐서 나타나는 확률 분포
* 서로 독립인 베르누이 시행을 n번 반복해서 실행 했을 때, 성공한 횟수 X의 확률 분포
* 베르누이 시행의 기댓값, 분산에 n만 ( n번 시행한 것이니) 곱해주면 된다

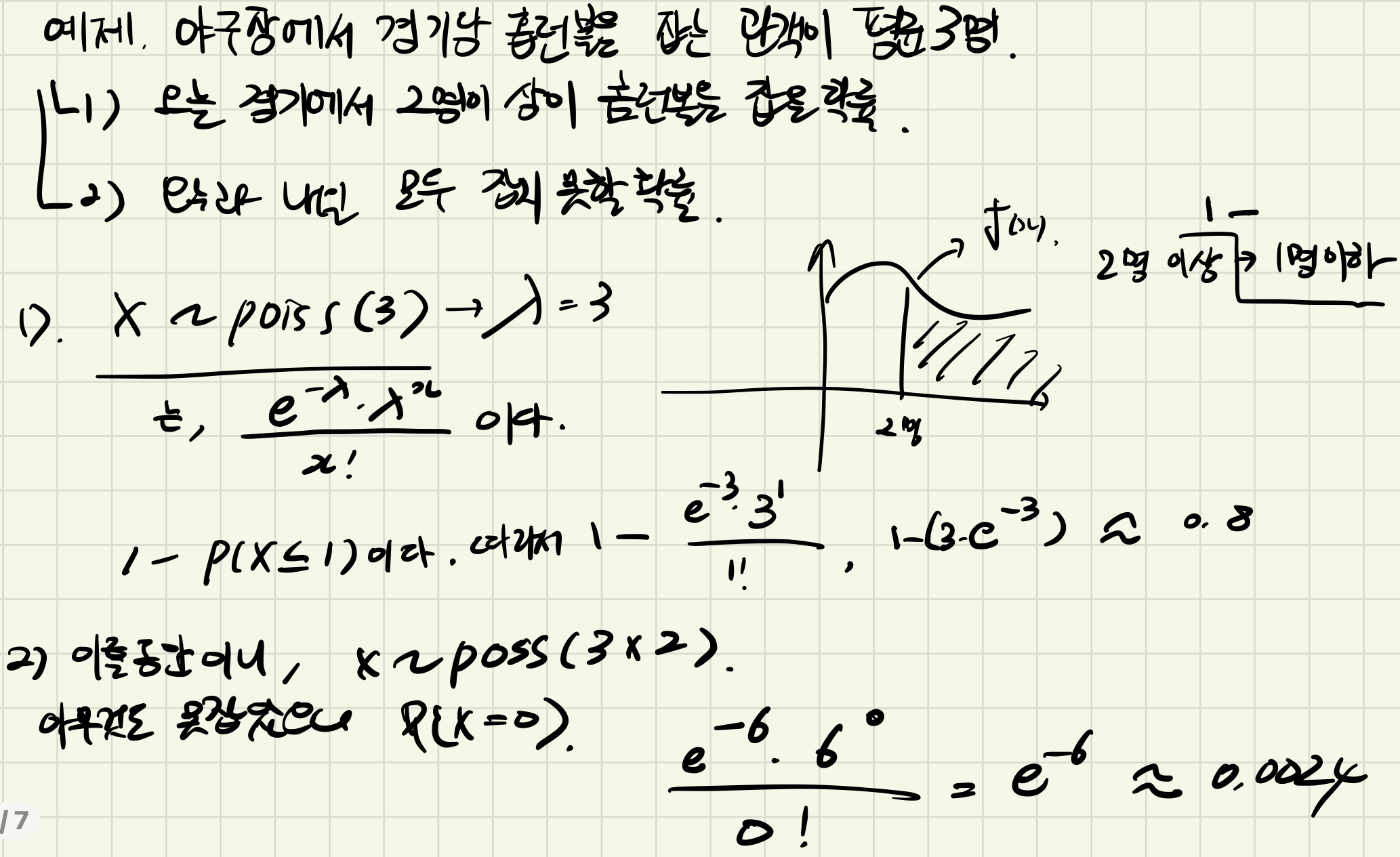
* 포아송 분포 ( Poisson distribution )
> 어늬 희귀한 사건이 어떤 일정한 시간대에 발생할 확률 분포로, 이항 분포의 특수한 형태
> ex ) 1년간 지구에 1미터 이상의 운석이 떨어지는 수
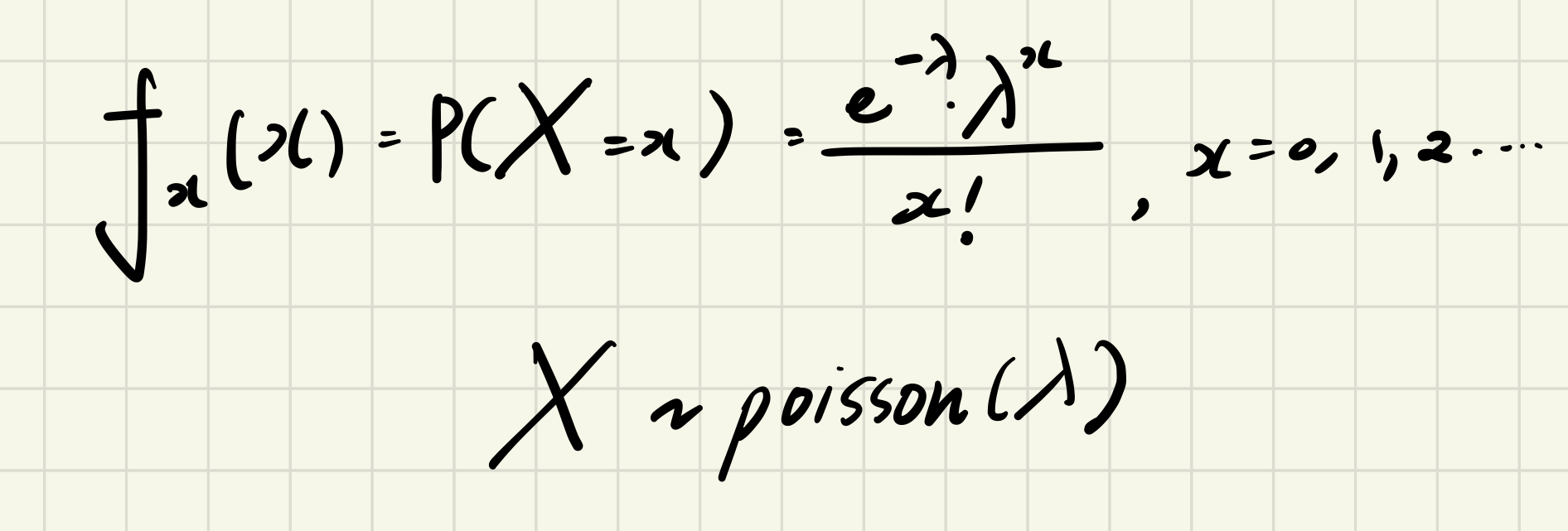
이항분포를 따르는 위와 같은 확률변수 X ~ B(n,p) 에서, n이 대단히 크고( 충분히 클 때 ) p가 대단히 작을 경우 np < 5 일 정도면
이 확률변수 X는 λ=np인 푸아송 분포로 근사할 수 있다.
* 이항 분포의 포아송 근사
> 보통 n이 클때, np<5를 만족할 정도로 p가 작으면 근사 정도가 좋다고 함 X ~ poisson(n,p)
> 이항 분포의 평균(기대값은) np , 포아송 분포의 평균(기대값)은 λ
> 그 값에 대입함으로써 근사 가능 , X ~ Poisson(np)
> ex) n = 100, p=0.01인 이항분포 X~B(100, 0.01) 을 포아송 근사하면 -> np = 100 * 0.01 , 즉 1 -> λ
> X ~ Poisson(1) 이 된다.
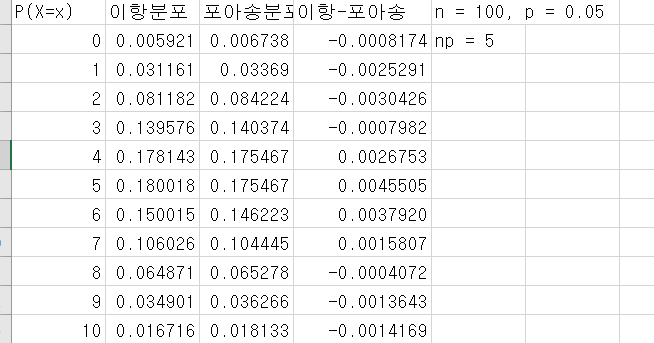
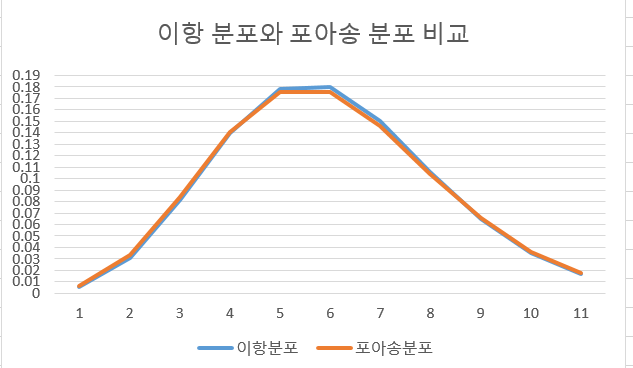
> 지금처럼 컴퓨터가 발달하지 않았을때 이항분포를 계산하지 못해서 유용했던 방법.
* 포아송 분포의 조건
> 희귀한 사건이 특정 시간대에 발생한 것이기 때문에, 어떤 단위구간이 있다고 할때, 이를 더 작은 단위 구간으로 나눌 수 있고, 이러한 짧은 단위구간 중에 어떤 사건이 발생할 확률은 전체 척도 중에서 항상 일정하다. ex) 1시간은 1시간끼리, 5분단위는 5분 단위간 발생확률은 일정
> 두 개 이상의 사건이 동시에 발생할 확률은 0에 가깝다
> 어떤 단위구간의 사건의 발생은 다른 단위구간의 발생으로부터 독립적임 ( 어떤 사건이 뒤의 사건에 영향을 주지 않는다 )
> 특정 구간에서의 사건 발생확률은 그 구간의 크기에 비례함. (60분에 한번 일어날 확률은 10분에 한 번 일어날 확률보다는 비례적으로 크다 )
> 포아송분포의 확률 변수의 기댓값과 분산은 모두 λ(람다)임.
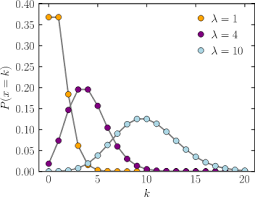
> 람다가 크면 정규분포에 가까운 모양 (그림 참고)
** 기하 분포 ( geometric distribution )
> 어떤 실험에서 처음 성공이 발생하기까지 시도한 횟수 x의 분포, 각 시도는 베르누이 시행을 따른다


** 음이항 분포 ( geometric distribution )
> 어떤 시행의 성공확률이 p일때, r번의 실패가 나오기까지 발생한 성공횟수 x에 대한 확률 분포
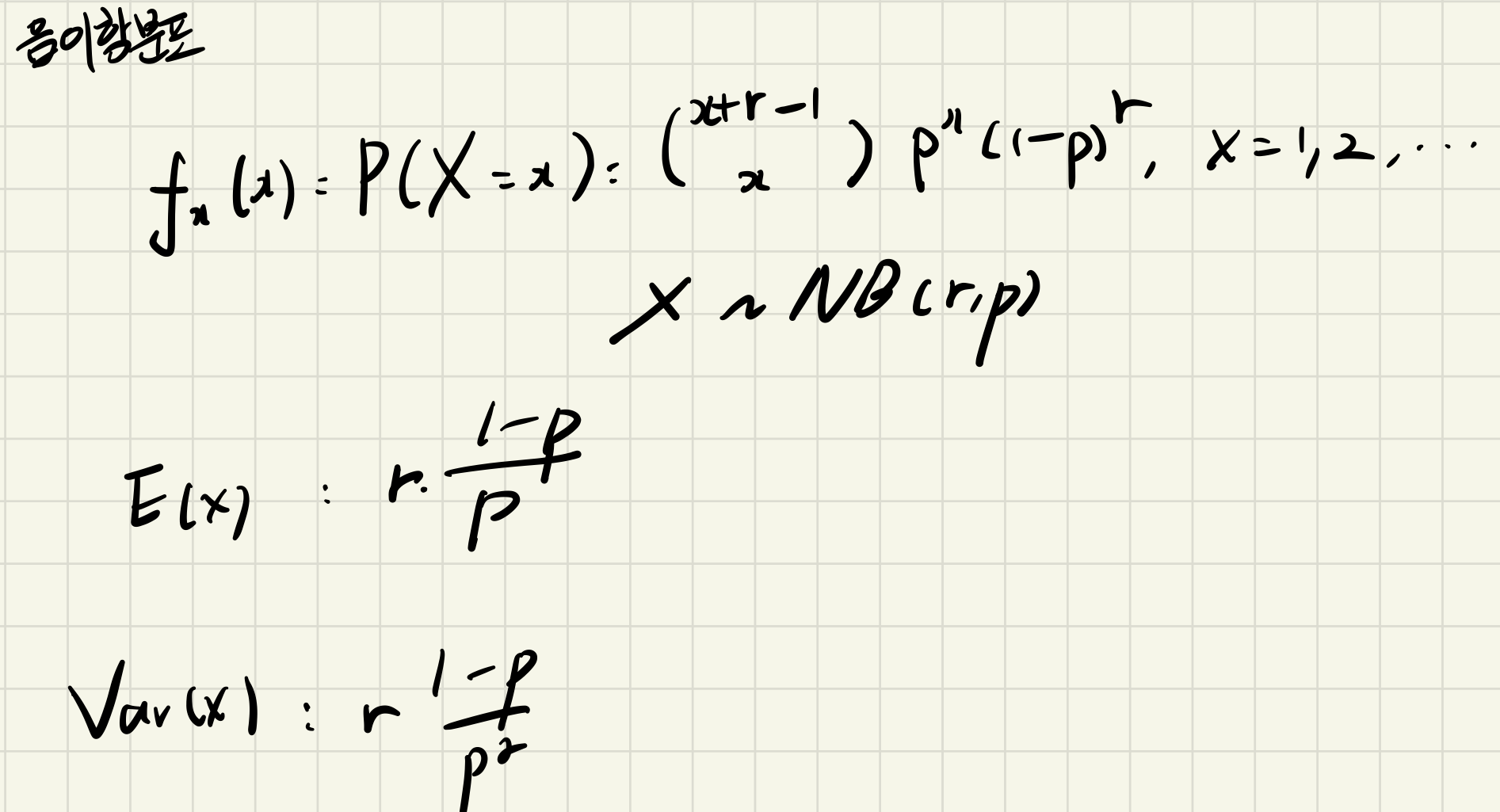
< Summary >

'BF 2024 > 통계' 카테고리의 다른 글
| 확률 분포들 간의 관계 (0) | 2022.02.14 |
|---|---|
| 연속형 확률분포 (0) | 2022.02.14 |
| 확률과 변수 (0) | 2022.02.13 |
| 확률 (0) | 2022.02.13 |
| 자료의 기초 통계량 (0) | 2022.02.11 |



