확률 본문
************************************************************************************************************
INDEX
** 확률
** 확률과 집합
** 베이즈 정리
************************************************************************************************************
** 확률 ( probability )
> 모든 경우의 수에 대해서 특정 사건이 발생하는 비율.
> 대체로 수학 외에서는 0과 1 사이의 소수 혹은 분수나 순열등으로 나타내기 보다는, 0과 100사이의 백분율(%)로 나타내거나 옛날 처럼 할푼리로 나타내기도 한다.
** 확률의 고전적 정의
> 확률에 대한 최초의 수학적 정의는 라플라스의 논문에 등장한다.
> 어떤 사건의 발생 확률은 그것이 일어날 수 있는 경우의 수 : 전체 가능한 모든 경우의 수이다.
> 단, 이는 어떠한 사건도 다른 사건들보다 더 많이 일어날 수 있다고 기대할 근거가 없을 때, 즉 모든 사건이 동일하게 일어날 수 있다고 할 때 성립한다. 정육면체 주사위에서 각각의 눈 수에 해당하는 사건은 동일하게 1/6으로 간주하는것 처럼.
** 표본 공간 ( Sample Space )
> 표본 공간이란 어떤 실험에서 나올 수 있는 모든 가능한 결과들의 집합
> 동전 던지기의 경우 S = {head, tail} , Dice S = {1,2,3,4,5,6}
> 사건 A가 일어날 확률은, A의 probability 즉 , P(A) 로 표기한다.
> 표본 공간 S가 유한 집합일때 표본 공간의 모든 원소들이 일어날 확률이 같으면
P(A) = 사건 A가 일어날 수 있는 경우의 수 / 표본공간 s의 원수의 수
** 통계적 확률 정의
> 어떤 시행을 N번 반복했을 때, 사건 A에 해당하는 결과가 r번 일어났을 경우 r/N 이고, 사건 A가 일어날 상대도수라고 한다
N이 무한히 커지면 상대도수는 일정한 수로 수렴하는데, 이 극한값을 lim r/N을 사건 A의 통계적 확률 또는 경험적 확률이라고 함.
> 예를들어, 동전을 10번 던졌을때 앞head이 3번 뒤tails가 7번 나왔다고 하자.
> Sample space의 크기는 10, {h,h,h,t,t,t,t,t,t,t} 이고, p(h) 와 p(t)는 3/10, 7/10 이 될것이다.
> 하지만 관측한 시행횟수 N을 무한에 수렴하도록 증가시키면 , 즉 동전을 허벌나게 많이 던졌을때 p(h)와 p(t)는 1/2로 수렴하게 될 것이다. 동전 던지기 시행에서 각각의 통계적 확률값은 1/2이다.
** 확률의 성질
* 합사건 , union : 사건 A또는 B가 일어날 확률
* 곱사건, intersection : 두 사건이 동시에 일어날 확률
* 배반사건, mutually exclusive event : 두 사건은 동시에 일어날 수 없는 경우
* 여사건 , complement : 사건 A가 일어나지 않을 확률

** 확률의 성질
> 덧셈 법칙 : p(A U B) = p(A) + p(B) - p(A n B )
> 배반 사건의 교집합은 공집합
> 사건 + 그 사건의 여집합 = 1 ( 사건이 일어날 확률과 일어나지 않을 확률을 더하면 1이다 )
** 순열과 조합
순열
https://dsjgm921.tistory.com/8
조합
https://dsjgm921.tistory.com/9
** 조건부 확률
> conditional probability : 어떤 사건 A가 발생했을 때, 또 하나의 사건 B가 발생할 확률
> 두 사건이 독립적인 사건 경우, P(A n B ) = P(A) * P(B)

> 어떤 사건이 발생했을때 또 하나의 사건이 발생할 확률이니, 당연히 선행 사건 A는 무조건 시행되었어야 한다. A > 0 그리고 분모의 자리에는 0이 올 수 없다.
> P(B|A) 는 A가 일어났을 때 B가 일어난 확률. 즉, 사후 확률이라고 볼 수 있다. 선행 사건 A는 사전 확률.
> 두 사건의 교집합과 사전-사후 확률의 관계는 다음과 같다. 베이즈 정리에서도 활용.
P(A n B) = P(B | A) * P(A) 그리고 P(A | B) * P(B)
-> P(A|B) = P(A n B ) / P(B)
** 베이즈 정리
> Bayes Theorem , 어떤 임의의 사건은 여러 변수의 확률 시행의 결합 형태로 볼 수 있다. 이때 우리가 알고 있는 현재의 사실은, 즉 관측한 사후 확률이다. 다만, 그 사건과 관련되어 사전에 알고 있는 어떤 사건의 확률 정보가 있다면(조건부로 선행된 사건의 확률) 이를 토대로 사건을 재구성 해볼 수 있다는 것.
> 대학원 수업에서 교수님은 굉장히 복잡하게 말씀하셨지만 다는 못알아들었고, 그때의 경험 역시 베이즈 정리와 같은 상황 아닐까.
> 쉽게는 "아만보"인 것 같다. 계속 추가적으로 정보를 Update 해가면서 재구성한다.
> 다만 전체 sample space를 알아야 한다는 것과, 각각의 시행은 배반사건이라는 전제가 있다.
> 각기 다른 7개의 물건중에서 하나를 뽑은 상황. 이때 손에는 두 개의 물건이 있을 수 없다.
> 또 7개의 물건을 각각 하나씩 뽑고, 이후 복원 추출했을 경우, A,B,C,D,E,F,G 각각의 통계적 확률은 1/7 이고, 배반사건의 합과 교집합 법칙에 의거 P(AUB) = P(A) + P (B) - P(AnB) 이지만, 교집합은 공집합이기에 전체 사건의 확률의 합은 1이 된다.
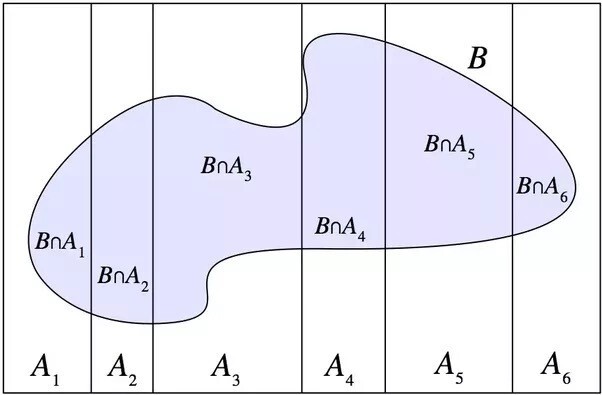
> 공식은 위의 연장선이니 따로 쓰지는 않겠다.
'BF 2024 > 통계' 카테고리의 다른 글
| 이산형 확률 분포 ( 균등, 베르누이, 이항, 포아송, 기하, 음이항 분포 ) (0) | 2022.02.14 |
|---|---|
| 확률과 변수 (0) | 2022.02.13 |
| 자료의 기초 통계량 (0) | 2022.02.11 |
| 데이터 이해와 기본적인 시각화 종류 (0) | 2022.02.11 |
| INTRO (0) | 2022.02.11 |


