연속형 확률분포

************************************************************************************************************

INDEX

연속형 확률 분포 

** 확률밀도함수란? ( probability density function ) 

** 누적분포함수란? ( cumulative density function ) 

** 연속형 확률 분포에서의 균일분포 ( uniform distribution ) 

** 정규 분포 ( normal distribution ) 
** 파라미터에 따른 정규 분포 모양 비교 

** 표준정규분포 ( standard normal distribution ) -> Z분포 
** 정규 분포의 성질

** 이항 분포의 정규 분포 근사 

** 지수 분포 

** 지수 분포의 무기억성과 문제 

************************************************************************************************************

 

<< 연속형 확률 밀도 함수 >>

 

** 확률밀도함수란? ( probability density function ) 

> 연속형 확률 변수 X에 대하여 함수 f(x)가 아래의 조건을 만족하면 확률 밀도함수라고 한다. 

> 확률 밀도 함수의 성질 ( 점의 값은 0 , -> 구간에서 이상/이하는 포함 안된다 ) 

 

** 누적분포함수란? ( cumulative density function ) 

> 확률밀도함수를 적분하면 누적분포 함수가 된다 

 

** 연속형 확률 분포에서의 균일분포 ( uniform distribution ) 

> 확률 변수 X가 a와 b사이에서 아래와 같은 확률 밀도 함수 ( pdf )를 같는다 

 

** 정규 분포 ( normal distribution ) 

> 가우스에 의해 제시된 것으로, 가우스 분포라고도 함 

** 파라미터에 따른 정규 분포 모양 비교 

 

출처 : &nbsp;위키&nbsp;

> 표준편차가 작을수록 평균에 몰려 있을 것, 클수록 자료의 거리가 머니 분산되어 있을 것 

> 평균이 이동하면 당연히 중심도 따라서 이동

 

** 표준정규분포 ( standard normal distribution ) -> Z분포 

> 비교를 위해서 데이터를 표준화할 때 필요한 작업 , 표준화 후 비교, 비교 후 원래 값을 다시 복원

 

출처 :&nbsp;http://www.ktword.co.kr/test/view/view.php?m_temp1=1995

 

> 정규 분포에서 표준편차 값에 따라서 구간의 확률밀도가 같았다.

> 표준 정규 분포는 표준편차 값으로 구간을 나누어준 것으로, 표준정규 분포에서 scale 1까지의 확률밀도 값 역시 정규분포와 같이 34.1%이다. 

 

** Standard Normal ( Z -value ) table

> auc에 해당하는 값으로 0과 z사이의 면적 즉 확률밀도함수의 값이다 

> 이상 ~ 이하에 따라 0이하 면적인 0.5를 더하거나 빼고 ... 

출처 :&nbsp;https://chukycheese.github.io/statistics/area-between-two-z-values-on-opposite-sides-of-mean/&nbsp;

 

** 정규 분포의 성질 

** 이항 분포의 정규 근사 

X  ~ B(n,p) 일 때, 확률 변수 X는 n이 충분히 크면 ( n > 30 ) 근사적으로 정규 분포 X ~ N(np,np(1-p))를 따른다.

 

출처 :&nbsp;http://databaser.net/moniwiki/wiki.php/이항분포-BINOMDIST?action=body

 

 

> 정규 분포의 공식에서 평균과 표준편차에 이항분포의 값을 넣음 

 

** 지수분포 ( exponential distribution ) 

> 단위 시간당 발생할 확률이 람다인 어떤 사건인 횟수가 포아송 분포를 따른다면, 어떤 사건이 처음 발생할때까지 걸린 시간 확률 변수 x는 지수 분포이다. ( 대기 시간의 분포가 지수 분포를 따른다  ) 

> 아래의 예시에서는 지구에 1미터 이상의 운석이 x개 0개 부터 1 , 1개부터 2, N-1 ~ N개 떨어지는데 걸린 각각의 대기 시간

https://dsjgm921.tistory.com/68

> 지수 분포는 x=0일때 매우 높을 수 있고, 이후 x+=에 따라 0에 근접한다. ( 지수 함수의 분포 형태를 갖는다 )   

> 지수 분포는 연속 되는 사건 사이의 대기 시간들도 지수 분포이다. 

wiki&nbsp;

** 지수 분포와 포아송 분포의 관계 

 

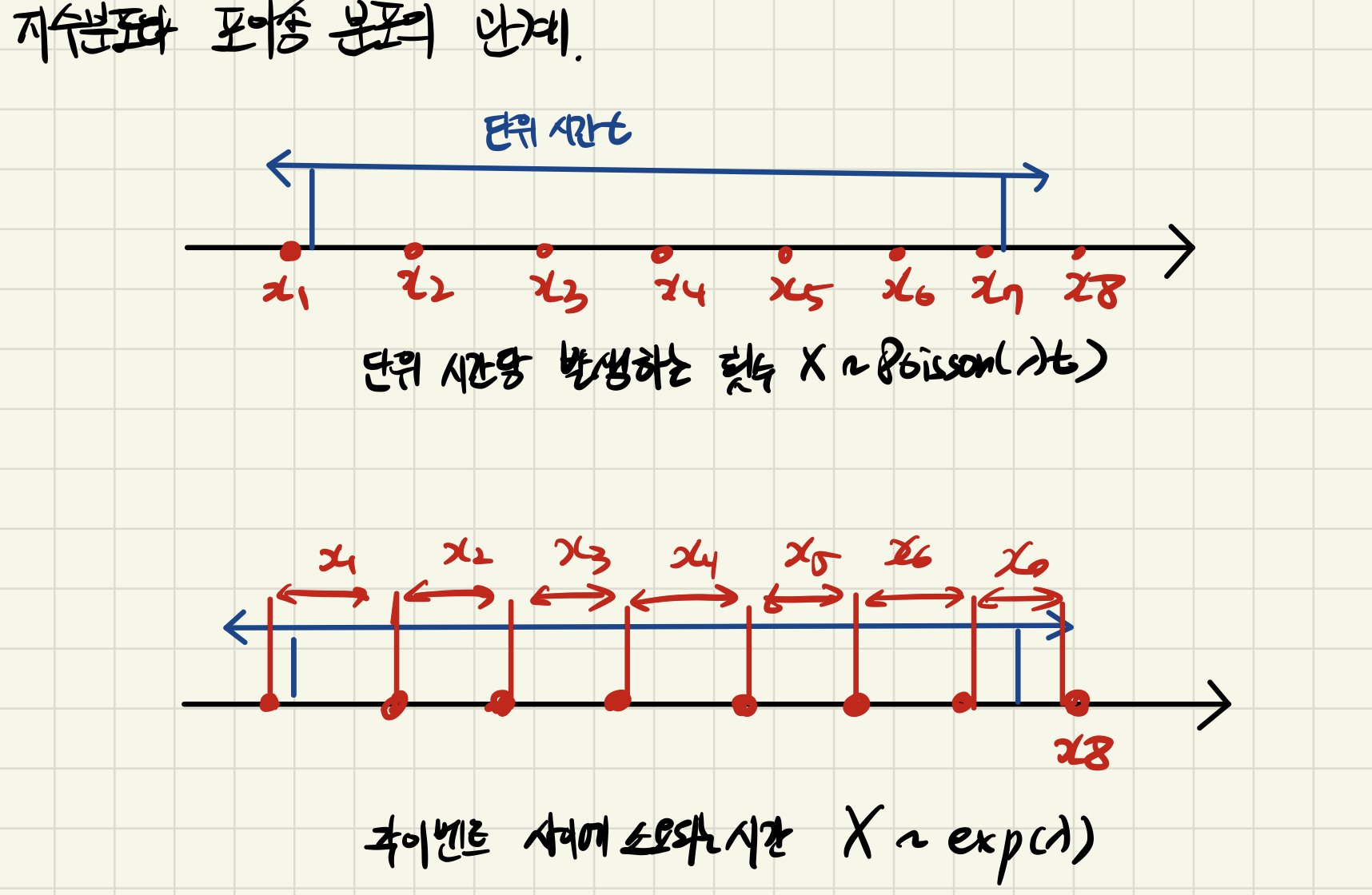
** 지수분포의 무기억성 ( Memoryless Property ) 

>  어떤 시점 부터 소요되는 시간은 과거 시간에 영향을 받지 않는다. 

> 버스를 이전 시간부터 기다렸던 사람이 있다고 해도, 내가 버스 정류장에 도착해서 대기할때의 대기시간은 같다 

> 전구를 한달 동안 사용 했을 때 남은 수명은 한달 간 사용했던 영향을 받지 않는다. 즉 새 전구와 한달 간 사용한 전구의 남은 수명이 같다고 생각하는 분포이다.

 

** 위의 어려움으로 실제 적용에는 다양한 문제가 있을 수 있다 

생존 분석에서는 Weibull 분포와 log-normal 분포를 사용하여 예측함