다중 회귀분석 본문
************************************************************************************************************
INDEX
** 단순 회귀 분석 이외에도 자주 쓰이는 회귀분석들
** 다중 회귀분석 (multiple regression analysis )
** 더미변수 ( dummy variables )
** 변수 선택법 ( 전진, 후퇴, 단계적 선택 )
** 다중공선성 문제와 VIF 분산팽창요인
** 해결법
************************************************************************************************************
** 단순 회귀 분석 이외에도 자주 쓰이는 회귀분석들
* 다중 회귀분석 (multiple regression analysis )
> 2개 이상의 독립변수로 종속 변수를 예측하는 회귀 모형을 만드는 방법
Y = B0 + B1X1 + B2X2 ...... BiXi + Ei
* 로지스틱 회귀분석 ( Logistic regression analysis )
> 반응 변수가 범주형(이진수)인 경우 사용하는 모형 , 주로 불량 예측이나 신용도 평가 에서 많이 쓰임
* 다항 회귀분석 ( Polynomial regression analysis )
> 독립 변수가 k개이고 반응 변수와 독립변수가 1차 함수 이상인 회귀분석
Y = B0 + B1x1 + B0(x1**2) ..
> 로그 함수로 확률을 표현 odds 비 p/1-p

* 다양한 모형들을 숙지하고, fitting에 가장 적합한 것을 선택하도록 하자. 선택지가 많아진다.
************************************************************************************************************
** 다중 회귀분석 (multiple regression analysis )
> 2개 이상의 독립변수로 종속 변수를 예측하는 회귀 모형을 만드는 방법
Y = B0 + B1X1 + B2X2 ...... BiXi + Ei
> 변수들 간 축척과 척도에 따라서 표준화가 필요하다
* 더미 변수 ( dummy variable )
> 값이 0 또는 1로 이루어진 변수
> 범주형 변수를 회귀분석에 사용하기 위해서는 더미 변수가 필요하다 ( binary, 0 or 1 )
> 하지만 구분을 1,2,3 등의 숫자로 하면 연속형 변수이기 때문에, 잘못 해석될 여지가 있으며 모형의 성능이 떨어지게 된다.
> 따라서 다음과 같이 더미 변수를 생성한다.
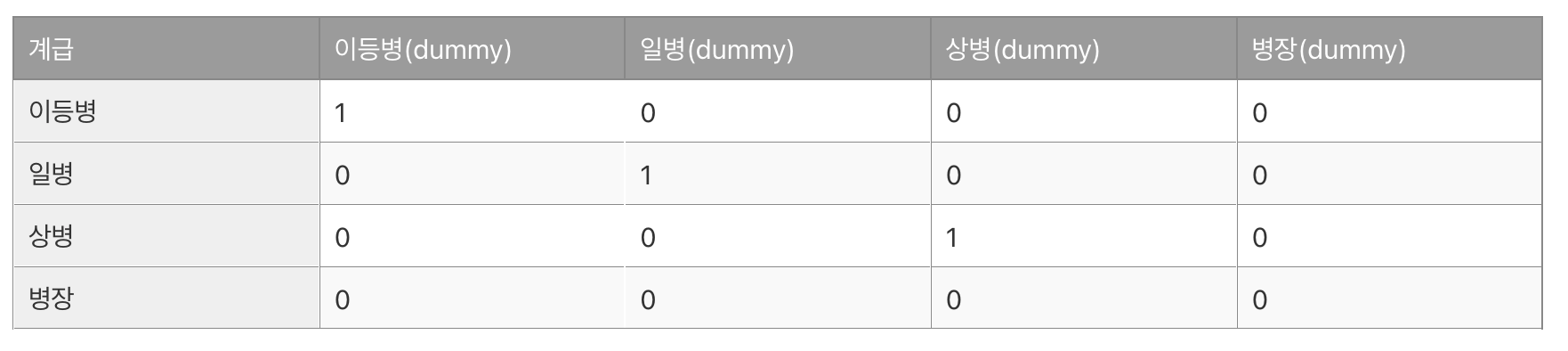
> 필요한 더미 변수의 개수는 범례의 수 -1 이다. 아래 예시의 경우 이등병~병장 총 4개의 범례이므로 -1 하여 3.
> 마지막 범례는 모두 0인 경우로 구성할 수 있기 때문이다.
범주 : { 이등병, 일병, 상병, 병장 }
잘못된 예시 (좌), 올바른 예시 (우) -> 더미변수임을 확실하게 표기해서 구분됨

* 결과 확인 , 변수 선택을 제외하고는 단순 회귀분석과 큰 차이는 없음
1) T 분포에서 변수의 유의성 p값 확인
2) 수정 결정계수 확인
3) 유의미하지 않은 변수 제거 후 다시 시행해보기
* 통계 패키지나 프로그램에 따라서 자동으로 범주형을 변환하기도 한다, 결과는 정상적으로 출력 된다
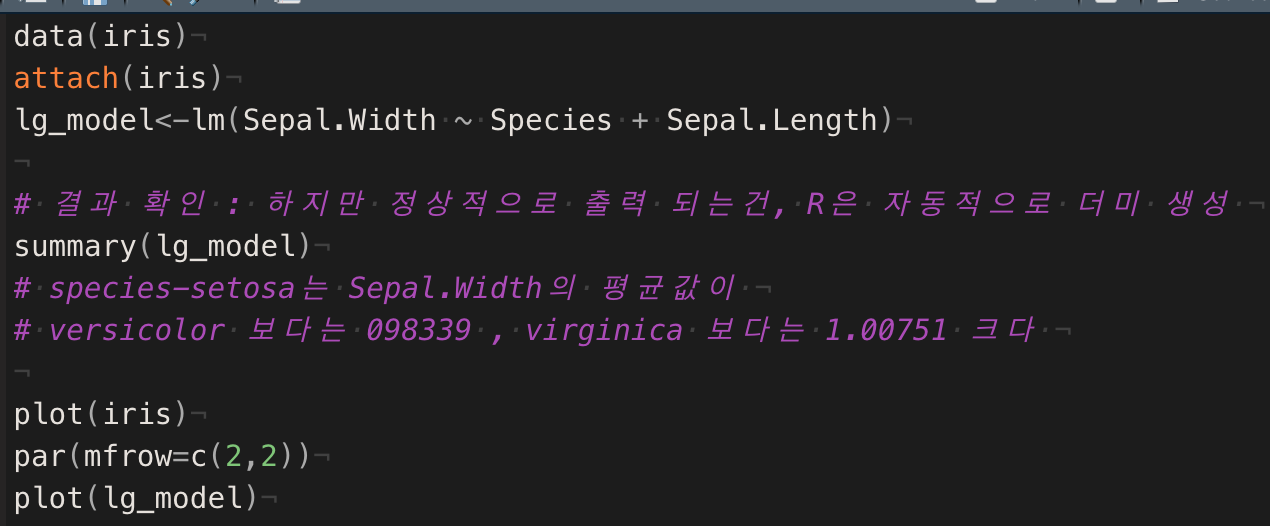
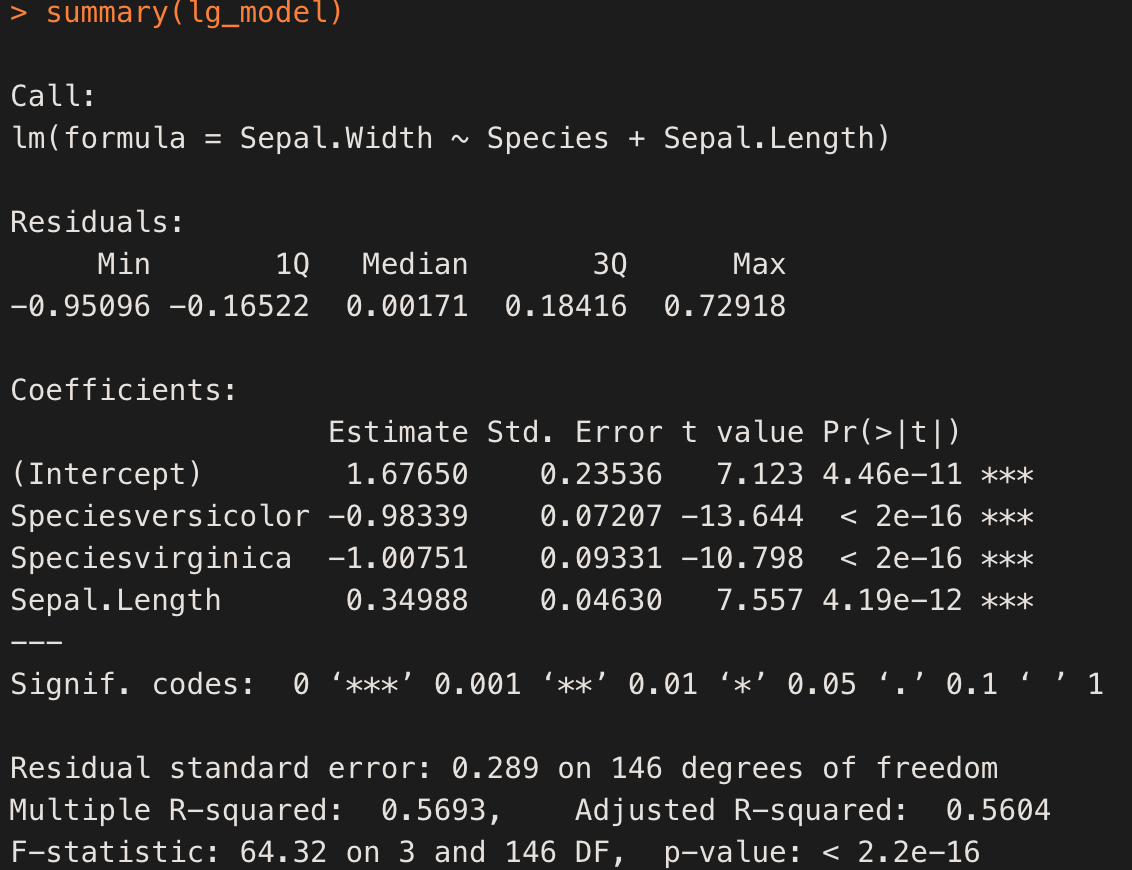
** 변수 선택법
* 전진선택법 ( foward selection ) : 독립변수를 1개부터 시작하여 가장 유의한 변수들부터 하나씩 추가하면서 모형의 유의성을 판단
* 후진제거법 ( backward selection ) : 모든 독립변수를 넣고 모형을 생성한 후, 하나씩 제거하면서 판단
* 단계적선택법 ( stepwise selection ) : 위의 두가지 방법을 모두 사용하여 변수를 넣고 빼면서 판단하는 방법
** 다중 회귀분석의 유의점
* 다중공선성 문제 ( Multicollinearity )
> 상관관계가 높은 독립변수들이 동시에 사용될 경우 문제가 발생
* 진단
> adj R**2 값이 높아 회귀식의 설명력은 높은데도 독립변수의 P-value가 커서 개별 인자들이 유의하지 않는 경우 의심
> 일반적인 경우에 VIF ( Variance Inflation Factor ) , 즉 분산팽창요인이 10 이상이면 다중공선성이 존재한다고 본다.
> VIF = 1 / ( 1 - k번째 변수가 종속변수일때의 R Sqaured ) , k번째 독립변수를 종속변수로, 나머지 변수들을 독립변수로 하는 회귀모형의 결정 계수
Y = B0 + B1X1 + B2X2 + B3X3 + .. 이 있을때, 예를들어 X3 = B0 + B1X1 + B2X2 ...으로 만든 후
분산팽창요인 VIF = 1 / ( 1 - (Rk번째 **2 ) 를 계산하는 것.
* 해결 방안
1) 다중공선성이 존재 하더라도 유의한 변수의 경우 목적에 따라서 사용할 수 있다 -> 무조건 들어가야하는 변수의 경우
2) 변수 제거
3) 주성분 분석으로 변수를 재조합 ( 차원 축소 ) -> 축소한 독립변수들을 제외하고 새로운 파생변수를 만들어 대체한다.
'BF 2024 > 통계' 카테고리의 다른 글
| 시계열 분석 (0) | 2022.02.17 |
|---|---|
| 분산분석 ( ANOVA ) (0) | 2022.02.17 |
| 단순 회귀분석 (0) | 2022.02.15 |
| 기본적인 통계분석의 갈래 , when what how (0) | 2022.02.15 |
| 범주형 자료 분석 (0) | 2022.02.15 |



