머신러닝에 필요한 선형대수 기본 지식들 본문
차례
1. 벡터 / 행렬
2. 고유값과 고유벡터
3. 스펙트럼 분해 ( eigenvalue decomposition ) / 특이값 분해 ( SVD : singular value decomposition )
1. 벡터 / 행렬
> 스칼라, 벡터 , 행렬 , 텐서

1. 벡터
> 벡터는 크기와 방향을 속성으로 가진다 , 서로 같은 벡터란 크기와 방향이 둘 다 같은 것
> 데이터 샘플들의 특징은 벡터로 표현된다. ex) 아이리스 데이터 셋의 행 벡터는 각각 꽃받침의 길이 ~ 등 값을 가지고 있다.


> 영벡터 : 모든 원소가 0인 벡터
> 일벡터 : 모든 원소가 1인 벡터
> 두 벡터의 곱은 내적 inner product / dot product 라고 한다.
> 2차 놈 norm 의 형태이다


> 단위 벡터 unit vector 란 길이가 1인 벡터로, 행렬의 각 값들을 2차 놈으로 나누어 준 것이다.
> 우측 이미지 참고, (e1)^2 + (e2)^2 = 1 이 된다
> 벡터의 선형 독립과 종속


> 선형 결합과 벡터 공간

> 벡터의 유사도

1. 행렬
> 행렬의 norm 은 프로베니우스 놈 frobenius norm 이라고 한다


> 정방행렬 : n x n OR m x m 처럼 행과 열의 개수가 같은 행렬
> 전치행렬 : transpose matrix, 모든 ( i,j ) 쌍에 대해 aij 원소를 aji 원소로 전치해놓은 행렬을 말한다
> 대칭행렬 : 행렬 A가 정방행렬이면서 A = A' ( A'T) 가 성립하는 경우 , 대각 요소들을 기준으로 대칭인 경우
> 대각행렬 : diagonal matrix , 행렬이 대각 요소만으로 이루어진 행렬
> 단위행렬 (unit matrix), 항등행렬 (identity matrix) : 대각 행렬에서 모든 대각요소가 1인 행렬
> 행렬의 곱셈에서는 결합,분배법칙은 성립하나 교환법칙이 성립하지 않는다
결 A(BC) = (AB)C
분 A( B + C ) = AB + AC
교 A*B != B*A
> 행렬식 ( Determinant )
n x n 정방행렬 A 의 행렬식은 |A| 혹은 det(A) 라고 표기하며, 하나의 실수 값으로 표현된다.
|A| = |A'| 이다
> 역행렬 ( inverse matrix )
AB = BA = I n을 만족시키는 행렬 B가 존재하면 , 행렬 B는 행렬 A의 역행렬이라고 하고, A^-1 로 표현한다.
A의 역행렬 = 1/|A| ( a22 -a12
-a21 a11 )
> 정칙행렬 ( nonsingular matrix )
역행렬이 존재하는 행렬 , 필요 충분 조건으로 |A| != 0 행렬식 값이 0이 아니다.
> 특이행렬 ( singular matrix )
행렬식이 0인 정사각행렬 ( |A| = 0 ) , 즉 행렬식과 역행렬이 존재하지 않는 경우
> 직교 행렬 ( orthagonal matrix )
정방행렬 A의 역행렬이 전치행렬 A'와 같은 경우
> 선형 독립인 열(행) 벡터의 수
* 행렬의 계수 ( rank )

2. 고유값과 고유벡터
> 행렬 변환 ( 벡터의 선형 변환 )
x -> Ta -> Ax , 변환된 행렬은 원래 행렬 x의 상이다.

> 비례 변환, 곱셈 변환, 반사 변환 , 선형 변환 등 .. 강의 자료 참고하자
> 교유값 ( EIgenvalue ) 와 고유벡터 ( EIgenvector )
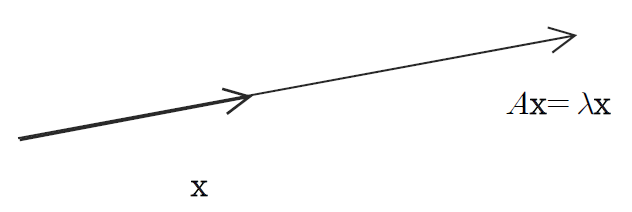
방향은 같고 크기만 바뀌는 변환을 생각해라
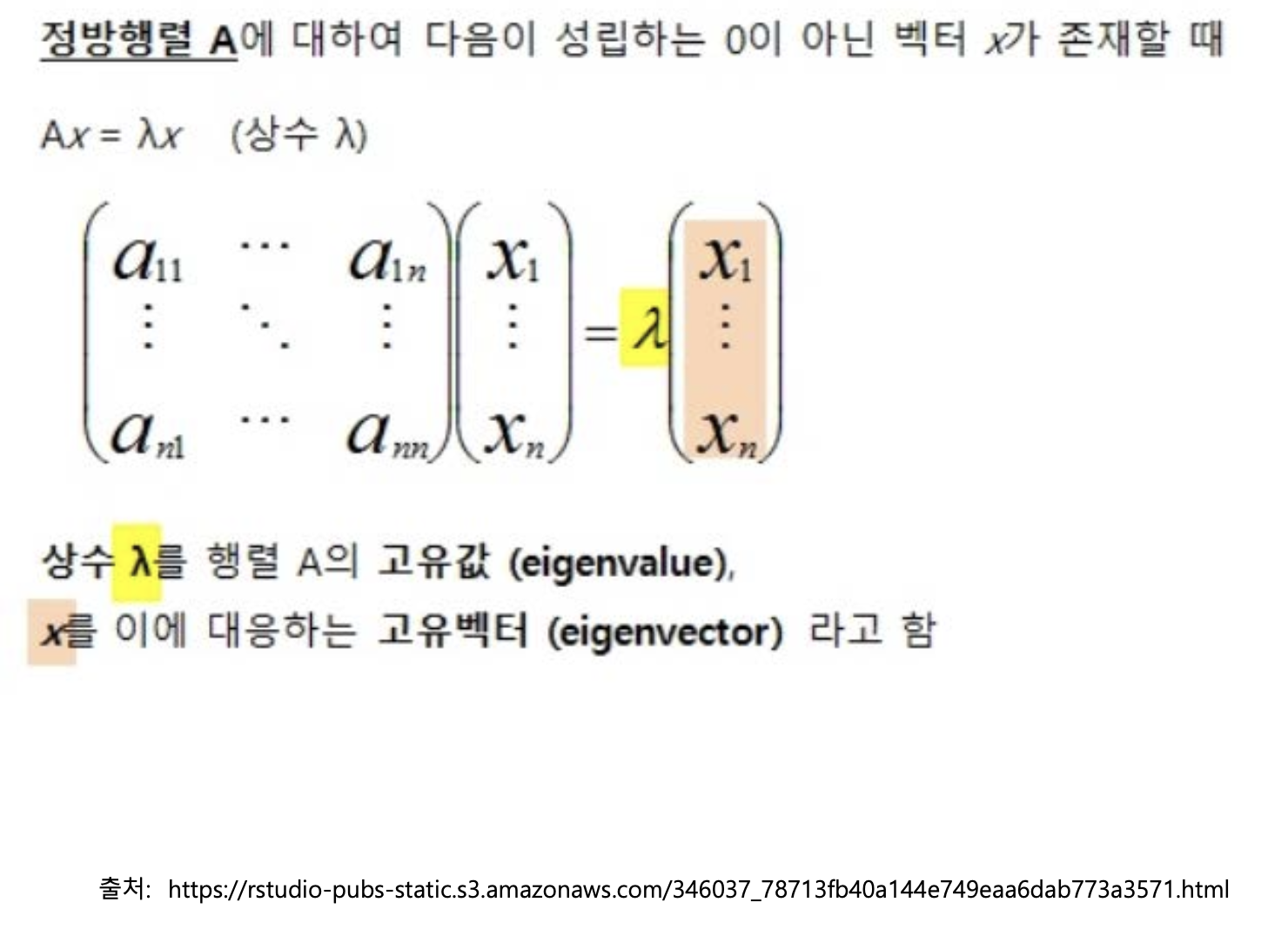
다음을만족할때 𝜆를A의고유값이라하고
x를 𝜆에 대응하는 A의 고유벡터라한다. ⇒ Ax=𝜆x
3. 스펙트럼 분해 ( eigenvalue decomposition ) / 특이값 분해 ( SVD : singular value decomposition )
> 행렬의 고유값을 구할 땐 행렬식을 사용한다
Ax=𝜆x -> (A-𝜆)x=0 인 상황
위 방정식이 0이 아닌 해를 가지려면 (A-𝜆) 은 sinular matrix 여야 하며 이때, det는 0이여야 한다.
|(A-𝜆)| != 0 이면 역행열이 존재하기 때문에 x 는 0이 되어 버린다 ( x는 영벡터가 아닌 경우 위배 ).
따라서 | (A-𝜆) | = 0 인 람다 값을 구하면 된다.
> 고유 벡터의 경우 찾아낸 람다 값을 통해 x1 x2 .. 값을 찾아낸다. 이후 x 행렬의 2차 놈 값을 통해 정규화 하면,그것이 무수히 존재하는 고유벡터 중 대표 값이라고 할 수 있는 e1 값이 된다.
> 두개의 정규화된 고유벡터의 내적은 0 이고 두 정규화된 정규벡터는 직교이며 독립이다.